Sons, imagens, vídeo, texto, tudo o que é processado em um computador se resume a uma sucessão de zeros e uns, a chamada linguagem binária. Até hoje, os computadores só conseguem entender que por determinado circuito está passando eletricidade ou não. O zero é a ausência de eletricidade, o um é a presença do sinal elétrico. Ligando e desligando microchaves, numa velocidade indescritível, é que o computador executa seu trabalho.

Temos dez dedos nas mãos, daí surgiram os números decimais. Você sabe, quando precisa representar 16, você diz dezesseis (dez-e-seis), ou seja, você faz uma marca que representa um dez e acrescenta à direita dela os seis restantes. E assim por diante. Mas, essa não é a única forma de contagem: na feira, você compra uma dúzia de bananas, duas dúzias e meia de laranjas etc. Nessa hora, você está fazendo uma conta na base 12, sabe que duas dúzias e meia de laranjas são o mesmo que 12+12+6, 30 laranjas. Bem, o computador faz algo parecido, ele traduz os números para a base 2, aquela dos zeros e uns, ligado e desligado.

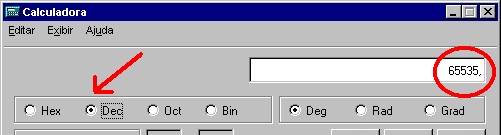
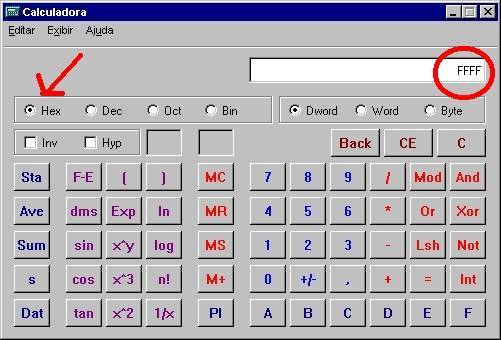
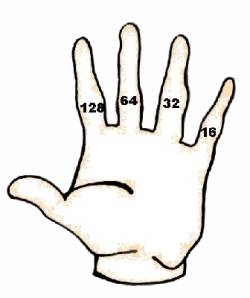
Para entender melhor, marque com uma caneta, no lado interno do dedo indicador da mão direita, o número 1. No dedo médio, escreva o número 2; no anular marque 4 e no mindinho marque 8.  Agora, baixe os dedos indicador e anular, de forma que estarão visíveis os números 2 e oito (cuja soma é dez). Na forma binária, os dedos levantados eqüivalem a 1 e os abaixados, a zero: você tem o número binário 1010, que vale o decimal 10.

Para transformar número binário em decimal, faça o contrário: baixe os dedos correspondentes aos zeros e deixe levantados os correspondentes aos uns, e some os valores dos dedos levantados. Verá que 0101 é o mesmo que o número decimal 5, por exemplo. Com apenas uma mão, você conta assim até 15. Para ampliar a contagem, use também a mão esquerda, com a palma voltada para você, marcando no mindinho o número 16, no anular o 32, no médio o 64 e no indicador o 128. Junte as duas mãos, lado a lado, e faça as contas. Nos dois casos, esqueça os polegares, faça como se não existissem.

Hexa - Alguns programas usam a linguagem hexadecimal, que é baseada num conjunto de 16 elementos: 0, 1 a 9, A até F.  Assim, o 15 do sistema decimal vale F em hexadecimal (ou 0F, já que o zero à esquerda também não tem valor), ou 1111 em código binário. Veja como é mais simples para o programador escrever um número em hexadecimal: um número que no sistema decimal precisa de cinco dígitos, como 65.535, e precisaria de dezesseis dígitos no sistema binário, pode ser escrito em hexadecimal com apenas quatro dígitos: FFFF).

A calculadora comum do Windows permite fazer a conversão de bases

A fórmula de cálculo dos números hexadecimais é parecida com o sistema decimal, você também multiplica o número pelo valor de sua posição, da mesma forma que no código decimal você sabe que 12 é um vezes 10, mais duas unidades. No cálculo hexadecimal, o número 2AF é calculado assim: o F equivale a 15, que é multiplicado pelo valor da posição (16 elevado a zero); o A equivale a 10 multiplicado pelo valor de posição (16 elevado a um) e o 2 equivale a 2 multiplicado por 16 elevado à potência 2. Faça as contas e terminará somando 15+160+512, total 687. Ou seja, 687 em código decimal é 2AF em código hexadecimal. Há também o código octal, que emprega dígitos de zero a sete para fazer as contas.

Nem vamos entrar em detalhes, mas é com esses códigos que se formam as palavras inteligíveis pelo computador, é por isso que você ouve falar tanto em bits (o caracter binário), bytes (palavras formadas com oito bits). Os números 16, 64 (oito ao quadrado), 256 (que é 16x16 ou 16 elevado ao quadrado), 1024 (um quilobyte vale 1024 bytes - e não mil bytes, como muita gente pensa: no código binário, a potência de 2 mais próxima de mil é 2 elevado à décima potência, que resulta em 1024). Muita coisa no computador é condicionada por números assim...